
A combat robot is designed to compete in an bulletproof arena against one or more opponents. Its main objective is to destroy the opponent. Even though it is an unusual application of engineering, this project stimulates creativity and requires a broad knowledge of various disciplines, which makes it an excellent learning tool.
MINOTAUR is a drum spinner and weights up to 115 kg. It causes damage to his opponents by transferring to them the kinetic energy previously accumulated on his spinning drum. Despite being designed to be balanced, the drum can be unbalanced due to imprecise machining or as result of combat damage.
I have conducted a study to determine the dynamic behavior of the robot as result to being submitted to a harmonic force (originated by the unbalanced drum), focusing on the following:
- Identifying the maximum unbalance that may exist before the robot is lifted off the ground (either on the wheels or on the front wedge).
- Identifying if the robot’s traction is impaired.
- Evaluating the force on the robot’s front interface with the floor.
To get the information needed to understand the robot, we need to choose a convenient way to model it. Our model should be close enough to reality to make a good prediction of the actual behavior. As the harmonic force generates forces in the lateral plane and the momentum is perpendicular to this plane, we can model the robot by representing it as a bar supported on two points. This is a convenient way of modeling because we transform our 3D problem into a 2D one.
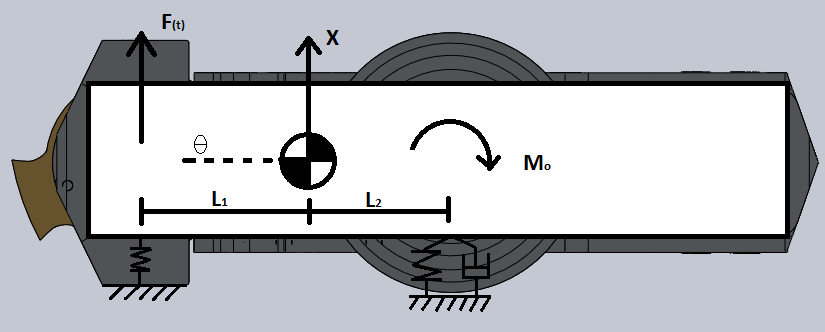
After a couple of mechanical tests and consulting the 3D model of MINOTAUR, I was able to determinate how we should model the robot’s interface with the ground and what values I should use for the moment of inertia and other characteristics. The final result was:
Representing this model as a state space system and simulating it allowed me to find some important results:
- Minotaur weapon motors were nowhere near reaching the natural frequency of the robot, so resonance would not be a problem.
- Only a small loss of mass [0.006 kg] on the tip of the drum can result in loss of contact with the ground on the front of the robot (if the robot is not accelerating).
- If the robot is reducing its velocity, the amount of mass necessary to lift the front of the robot is much bigger [0.017 kg], almost three times more than before. This leads us to conclude that whoever is driving the robot can compensate for the damage on the drum by decelerating on key moments.
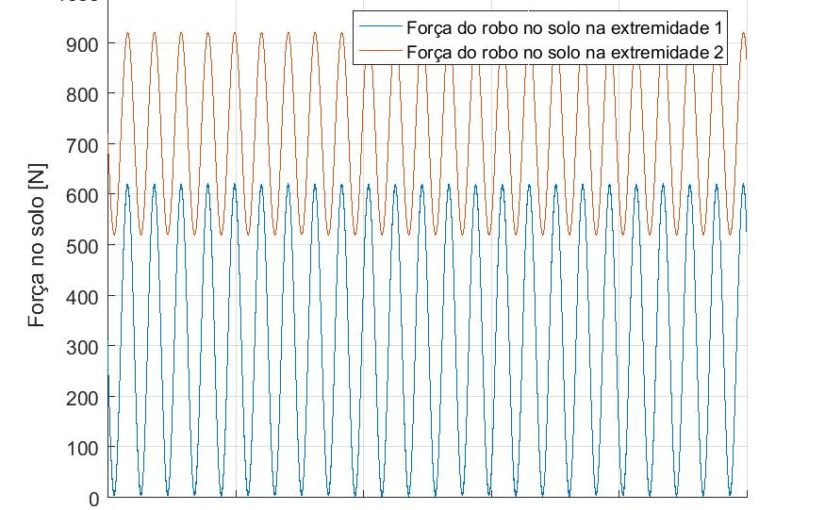
- The following graph show us the forces the robot would apply to the ground while suffering the harmonic forces. The red line corresponds to the front of the robot, and the blue line to the wheels.
We can easily observe that even when the unbalance is not critical (it doesn’t lift the front nor the wheels from the ground), it has a major impact on the amount of traction the robot has, therefore being prejudicial, and it should be avoided if possible.